Algebra考点分析(五)函数和数列
Algebra代数部分在GMAT数学中仅次于算术部分,是第二大考点和难点。代数部分主要包括代数式、方程、不等式、幂、绝对值和函数几个考点。今天我们来看一下函数和数列部分的一写难点。
一、函数和数列的定义
给出一个关于x的代数式就能定义一个关于x的函数,用f(x)来表示。例如:
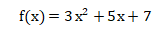
这就是一个关于x的函数。代入任意x的取值都能对应出一个f(x)的值。
如果x取值只包含正整数及0,那么使x=0,1,2,3。。。所得到的对应的f(x)就能形成一个数列。
在函数和数列的部分主要会考到两个方向:
1.函数和数列的定义,即一个x对应一个f(x)的对应关系。
2.等差数列和等比数列的性质。
今天我们主要来看一下第一个方面:对于函数定义的考察。
二、例题
【例一】
For each positive integer k, let 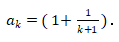 . Is the product
. Is the product 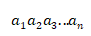 an integer?
an integer?
(1)n+1 is a multiple of 3.
(2)n is a multiple of 2.
这个题目里定义了一个数列,要求数列的前n项的乘积。那么我们先把前n项的乘积表示出来看一下有什么规律:
product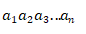
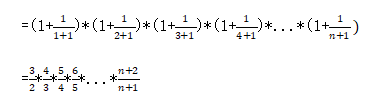
乘到这里就会发现,前一项的分子和后一项的分母是可以约掉的,所以最后得到
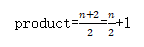
所以要判断product是不是整数,就变成了判断n的奇偶性。
条件(1):n+1是3的倍数,表示为n+1=3a,n=3a-1,n的奇偶性无法判断,不充分;
条件(2):n是2的倍数,n一定是偶数,那么product一定是整数,充分。
因此这个题选B。
当题目里定义了某个函数或数列时,只需要按照定义去写出来这个函数或数列,再去寻找规律就可以了。















 400-1816-180
400-1816-180


































 12G备考资料
12G备考资料